- Вы можете помочь с ежемесячной оплатой облачного хранения файлов или приобретения жестких дисков для хранения.
- На сайте регистрация закрыта, для регистрации на Форуме используйте данную форму.
Изометрическая проекция
 В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика могли быть использованы для представления трёхмерной игровой среды - поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования зрительной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.
В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика могли быть использованы для представления трёхмерной игровой среды - поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования зрительной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.
Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики - линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctg 0,5 ≈ 26,565° к горизонтали. Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические. Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины ''вид 3/4'' и ''2.5D''.
Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout и SimCity 4, в которых используется триметрическая проекция, были отнесены к ''изометрическим''. Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past и Ultima Online, а также игры с перспективной проекцией с видом ''с воздуха'', такие как The Age of Decadence и Silent Storm, также иногда относят к изометрическим или ''псевдо-изометрическим''.
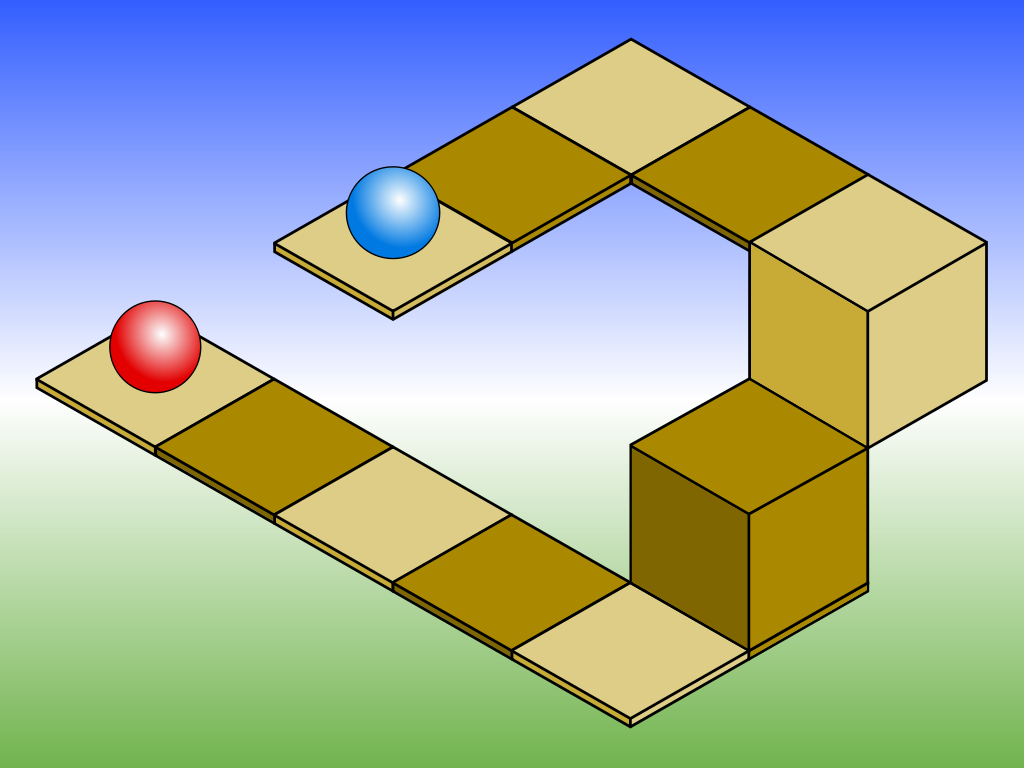
Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome. Слоган игры - ''В этом мире то, что ты видишь, становится реальностью''. 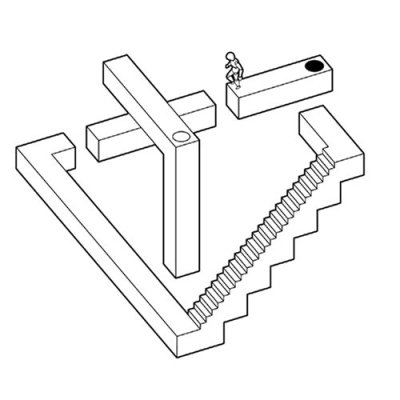 Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто ''перешагнуть'' с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек ''перешагнул'' на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае - под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.
Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто ''перешагнуть'' с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек ''перешагнул'' на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае - под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.
Первыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert и Zaxxon выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo, работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).
С выходом Ant Attack (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории ''графика'' за новую ''трёхмерную'' технологию. Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение, определившее последующий жанр изометрических квестовых игр. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar. Среди клонов большой успех имела игра Head Over Heels (1987). Однако, изометрическая проекция не ограничивалась только аркадами и квестовыми играми - например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.
На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр - начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу. (Далее на Wikipedia)
 Как и в знаменитых видеоиграх типа Pink Panther и
Как и в знаменитых видеоиграх типа Pink Panther и  Ваша задача заключается в том, чтобы создать лучший в мире "Парк Культуры и Отдыха"! Это совершенно потрясающая
Ваша задача заключается в том, чтобы создать лучший в мире "Парк Культуры и Отдыха"! Это совершенно потрясающая  Q*bert - аркадная игра, созданная Уорреном Дэвисом и Джеффом Ли и изданная компанией Gottlieb в 1982 году. Эта игра стоит у истоков применения изометрической проекции в играх, а её следы встречаются в кино, на телевидении, в музыке, в книгах и других играх. В игре Q*bert игрок гоняет одноимённого персонажа по изометрической пирамидальной структуре из трёхцветных кубиков. Цель Q*bert - прыгая по верху этих кубиков, перекрасить их в заданный цвет (к примеру, из голубого в жёлтый). Q*bert-у мешают разнообразные враги. Змейка Coily появляется сверху пирамиды внутри фиолетового шара, спрыгивающего по направлению вниз. Как только шар попадает на нижний ряд кубиков, змейка выскакивает из него и начинает прыгать по всей пирамиде в погоне за маленьким оранжевым героем.
Q*bert - аркадная игра, созданная Уорреном Дэвисом и Джеффом Ли и изданная компанией Gottlieb в 1982 году. Эта игра стоит у истоков применения изометрической проекции в играх, а её следы встречаются в кино, на телевидении, в музыке, в книгах и других играх. В игре Q*bert игрок гоняет одноимённого персонажа по изометрической пирамидальной структуре из трёхцветных кубиков. Цель Q*bert - прыгая по верху этих кубиков, перекрасить их в заданный цвет (к примеру, из голубого в жёлтый). Q*bert-у мешают разнообразные враги. Змейка Coily появляется сверху пирамиды внутри фиолетового шара, спрыгивающего по направлению вниз. Как только шар попадает на нижний ряд кубиков, змейка выскакивает из него и начинает прыгать по всей пирамиде в погоне за маленьким оранжевым героем. В войне синдикатов (Syndicate Wars) Вы можете встать на сторону Церкви Новой Эпохи, превратившись в ее адепта и признав святого Шодака своим Наставником. Вашим подспорьем станут священный Кодекс и изучающая и преумножающая его Девятка. И пусть Книга Катаклизма ведет Вас в Ваших завоеваниях, а мудрость Девятерых поможет Вам спасти этот мир. Из всех адептов Церкви именно Вы выбраны для борьбы с проклятым Синдикатом. Именно Вы знаете, каким должен быть этот мир и не позволите богомерзкому ЕвроКорпу осквернить его. Посмотрите вокруг: люди лишены веры, чувства справедливости, почтения к святыням. Все они запрограммированы дьявольской корпорацией и верят, что живут в солнечной и цветущей сказке. Но это не так!
В войне синдикатов (Syndicate Wars) Вы можете встать на сторону Церкви Новой Эпохи, превратившись в ее адепта и признав святого Шодака своим Наставником. Вашим подспорьем станут священный Кодекс и изучающая и преумножающая его Девятка. И пусть Книга Катаклизма ведет Вас в Ваших завоеваниях, а мудрость Девятерых поможет Вам спасти этот мир. Из всех адептов Церкви именно Вы выбраны для борьбы с проклятым Синдикатом. Именно Вы знаете, каким должен быть этот мир и не позволите богомерзкому ЕвроКорпу осквернить его. Посмотрите вокруг: люди лишены веры, чувства справедливости, почтения к святыням. Все они запрограммированы дьявольской корпорацией и верят, что живут в солнечной и цветущей сказке. Но это не так! Однажды на деревню нападает Человек-Ящерица (Lizard Man), все в панике, но тут появляется Бомбермэн и побеждает злодея. По этому поводу сельчане устраивают праздник и возводят Бомбермэна на трон. Спустя годы, уже старый Король, находясь на балконе своего дворца, видит предзнаменование: Тёмный Бомбермэн собирает свои силы чтобы завоевать мирное королевство. Король собирает свою армию, чтобы дать достойный отпор агрессору. Королю Bomber-у предстоит отвоевать свои земли и, в конечном счете, сразится с главным злодеем Bagular и его четверыми подручными.
Однажды на деревню нападает Человек-Ящерица (Lizard Man), все в панике, но тут появляется Бомбермэн и побеждает злодея. По этому поводу сельчане устраивают праздник и возводят Бомбермэна на трон. Спустя годы, уже старый Король, находясь на балконе своего дворца, видит предзнаменование: Тёмный Бомбермэн собирает свои силы чтобы завоевать мирное королевство. Король собирает свою армию, чтобы дать достойный отпор агрессору. Королю Bomber-у предстоит отвоевать свои земли и, в конечном счете, сразится с главным злодеем Bagular и его четверыми подручными.